Peter Geach, Reason and Argument XIV (mit deutscher Übersetzung)

14. Turning Sound Arguments into New Arguments (Themata)

In the last two chapters we have been concerned with patterns of argument, sound and unsound. We shall now be concerned with methods for turning kinds of sound argument we already have into new sound arguments. The Stoic logicians called such a rule or method a thema — plural themata. This is a short word you can use if you wish: do not confuse themata, which are methods for forming arguments out of arguments, with argument schemata, which are patterns for inferring propositions from propositions. The starting-points and results are different. An argument, whose pattern is an argument-schema, starts from premises and ends with a conclusion. Any premise or conclusion is itself not an argument but a proposition — whether an asserted proposition or one just assumed for the space of the argument. No proposition is ever itself an argument; so a procedure for passing from one or more arguments known to be sound to the formulation of another sound argument is not itself an argument from premises to conclusion. That’s why it is best to have a special name for such procedures.

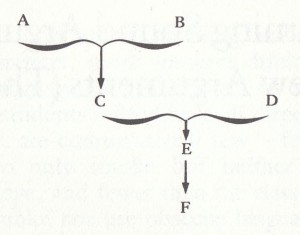
(1) The simplest sort of thema is the chainlike ordering of arguments: whatever follows from a conclusion follows from its premises. If we have a sound argument from A and B to C, and another from C and D to E, and another from E to F, then we have a sound argument from A, B, and D to F.

As I said before, a physical chain may break either because it has a weak link or because it is too long: a logical chain can break only for the first reason — if (but only if) each link is sound, the whole chain is sound.

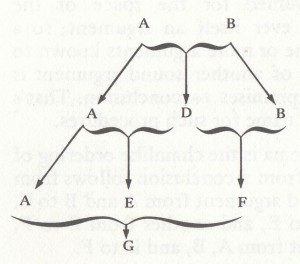
(2) The synthetic rule (discovered by pupils of Aristotle). This is an elaboration of the chain rule. Any conclusion drawn from our original stock of premises may be added to our premises to get new conclusions, and this increase in our stock may be repeated ad lib, all the conclusions thus reached are counted as conclusions from the first stock of premises. E.g. we may get D from A and B, then E from A and D, then F from B and D, then G from A, E and F; D, E, F, and G all follow from A and B; so we need no longer have the neat tree-like pattern of Rule (1).

Notice that we repeat (or reiterate, as the technical term is) the use of A and B as premises; the arrows from A to A, or B to B, are all right, because obviously any proposition follows from itself.

The working of the synthetic rule depends on the fact that no addition to a stock of premises can stop a conclusion from following: whatever follows from B and C follows still if we add a new premise D.

The synthetic rule may not always have seemed obviously sound: in an obscure passage of the Phaedo Plato complains of ‘enemies of reason who confuse together a first principle and the things derived from it’. Anyhow, in fact the question whether A follows from B and C does not in any way depend on how we got our B and C, nor on whether these are ‘first principles’ or not, nor on what other information we have besides B and C.

(3) Rules (1) and (2) only tell us how to fit arguments together to make a longer one: the other rules we are to study tell us how to get arguments with different premises and/or conclusions from arguments we already have.

Rule (3) is the rule for using reductio ad absurdum, which we’ve already looked at in Ch. 6 (Uses of argument). If premises, P,Q,R, . . . lead together to a contradiction, we do not (if we are sensible) conclude that we have proved a contradiction — rather, that there is something wrong with the premises. So if we retain Q,R, … we may derive from these the negation or contradictory of the remaining premise P. We have had such a move already in Chapter 13. Since the premises:

Most As are Bs; most Bs are Cs; most Cs are As; no A is BC together yield a contradiction, it follows that from the premises:

Most As are Bs; most Bs are Cs; most Cs are As

we can infer the contradictory opposite of the remaining premise ‘No A is BC’, namely:

Some A is BC.

In general, logic does not tell us which premises we are to keep and infer that the remaining one must be rejected. (If the boat is sinking, someone may have to go overboard, but logic need not tell us who.)

(3A) From this rule we may derive a rule of contraposition which is often useful. If from A and B we could infer C, then from A and the negation of C we can infer the negation of B. For if C follows from A and B, then this set of premises:

A, the negation of C, B

leads to a contradiction — the negation of C (in the set already) plus C (derivable from A and B). So if we keep A and the negation of C as premises, we must reject B and infer the negation of B.

(4) A rule that looks almost too obvious to mention: Suppose that if we had premises A,B,C … we could infer conclusion P. Now suppose that we lack one of these premises, say B and that P doesn’t follow from A,C, . . . All the same, we know that something follows from A,C, . . . just as they are: namely, the conditional formed with B and P — we know that from A,C, … it follows that if B is true then P is.

Example: From the premises:

All books on that shelf are blue; there’s a copy of Caesar among the books on that shelf

we obviously get the conclusion ‘There’s a blue copy of Caesar on that shelf’

(It’s obvious; but, for practice, work out a proof of this with the diagrams.)

From this we learn that from the single premise ‘All the books on that shelf are blue’ we can infer the conclusion:

If there’s a copy of Caesar among the books on that shelf, then there’s a blue copy of Caesar among the books on that shelf.

From this it is clear that the argument you get by applying rule (4) — called by logicians the conditionalizing rule — is different from the argument you started with. In the example, the original argument has two premises, and the conclusion is that there is a blue copy of Caesar on the shelf: the argument got by the conditionalizing rule — which must be sound if the argument we started with was sound (as it was indeed) — has one premise; and there is an ‘if’ in the conclusion, unlike the original conclusion.

(5) Dilemma. This is one of the few technical terms of logic that come up in ordinary language in a sense roughly corresponding to their logical meaning. It shows a way of plaiting together two arguments that reach the same conclusion along two different routes.

Suppose we have the conclusion P following by a sound argument from A,B,C, . . . and also from D,E,F, . . . Now suppose we’re not given A as a premise, and not given D as a premise either, but are given as a premise that either A holds or D does. Then from this information together with the remaining premises — B,C, . . . plus E,F, … — we can infer the conclusion P. On one alternative, P follows from A,B,C, . . . and on the other from D,E,F, . . . ; so anyhow it follows from B,C, . . . plus E,F, . . . plus the ‘either/or’ premise.

Example:

P.: Either B will drink the water or he will not.

Alternative (i)

Q.: B will drink the water in his water-bottle.

R.: The water in B’s water-bottle is saturated with salt, and B is severely dehydrated.

S.: Anybody who drinks water saturated with salt and is severely dehydrated dies of thirst.

Therefore

T.: Bill will die of thirst.

Alternative (ii)

V.: B will not drink the water in his water-bottle.

W.: If B does not drink the water in his water-bottle B will get no water in the desert.

X.: If B gets no water in the desert, B will die of thirst.

Therefore

T.: Bill will die of thirst.

By Alternative (i) we have T following from Q,R, and S; by Alternative (ii) we have T following from V,W, and X. Since P (which says that either Q or V is true) is obvious anyhow, we have T following from the set of premises R,S,W, and X — even if we don’t know which one of the premises Q,V, is true.

14. Gültige Argumente in neue Argumente (Themata) verwandeln

In den letzten beiden Kapiteln galt unser Interesse Mustern von Argumenten, gültigen und ungültigen. Nun lernen wir Verfahren kennen, mit denen wir bestimmte Arten von gültigen Argumenten, die wir bereits geprüft haben, in neue gültige Argumente verwandeln können. Die stoischen Logiker nannten solch eine Regel oder Methode ein thema, Plural: themata. Mit diesem kleinen Wort lässt sich eine große Sache treffend bezeichnen. Doch sollten wir themata, also das Verfahren, Argumente aus Argumenten zu bilden, nicht mit den logischen Schemata verwechseln, die uns dazu dienen, Aussagen aus Aussagen abzuleiten. Ausgangspunkte und Ergebnisse beider Methoden sind unterschiedlich. Ein Argument, dessen Muster ein Argument-Schema darstellt, beginnt mit Prämissen und mündet in eine Konklusion. Prämissen und Konklusionen sind für sich genommen keine Argumente, sondern Aussagen – ob nun ausdrücklich bejaht oder hypothetisch zum Zweck der Argumentation in den Raum gestellt. Keine Aussage ist jemals selbst ein Argument und kann nicht rein argumentativ verwendet werden. Ein Verfahren, mit dem wir als gültig erwiesene Argumente in neue gültige Argumente transformieren, ist nicht selbst wiederum ein Argument aus Prämissen und der Konklusion. Deshalb tun wir gut daran, dieses Verfahren mit einem eigenen Namen zu belegen.

(1) Die einfachste Form eines Themas besteht in der kettenförmigen Anordnung von Argumenten. Was immer aus einer Konklusion folgt, folgt naturgemäß auch aus ihren Prämissen. Wenn wir ein gültiges Argument aus A und B nach C haben und ein anderes gültiges Argument aus C und D nach E und noch ein gültiges Argument aus E nach F, dann verfügen wir über ein gültiges Argument aus A, B und D nach F.

Wie ich zuvor schon sagte: Eine materielle Kette bricht, sei es, weil sie ein schwaches Glied hat, sei es, weil sie zu lang ist. Dagegen bricht eine logische Kette oder der Strang unserer Argumentation nur aus ersterem Grund – dann (und nur dann), wenn alle Glieder der Kette gültig sind, hält das ganze Stück (so lang es immer sein mag).

(2) Die Regel der Synthesis (von Schülern des Aristoteles aufgestellt). Diese Regel ist eine Ausarbeitung der obigen Kette von Argumenten. Wir fügen neue Prämissen an den Vorrat unserer bekannten Prämissen und erhalten so neue Konklusionen. Dieses Verfahren methodischer Zunahme der Argumentation kann nach Belieben verlängert werden: Alle auf diesem mitunter sehr langen Wege erreichten Schlussfolgerungen gelten als Schlussfolgerungen aus unseren ersten Prämissen. So erhalten wir zum Beispiel aus A und B die Folgerung D, dann aus A und D die Folgerung E, sodann aus B und D die Folgerung F, und schließlich gelangen wir von den Prämissen A, E, und F zur letzten Folgerung G. Die Aussagen D, E, F und G folgen alle aus den ersten Prämissen A und B. Das hübsche baumartige Muster der Regel (1) brauchen wir nicht mehr, um zu diesem Ergebnis zu kommen.

Beachte: Wir wiederholen (oder reiterieren, wie der Fachterminus heißt) die Verwendung A und B als Prämissen. Die Bögen von A nach A und von B nach B sind ganz in Ordnung, schließlich folgt jede Aussage evidentermaßen aus sich selbst.

Das Funktionieren der Regel der Synthesis hängt von der Tatsache ab, dass wir beliebige Prämissen unserem bestehenden Vorrat an Prämissen hinzufügen können, ohne dass uns dabei gültige Konklusionen verlorengingen. Was immer aus B und C folgt, es folgt weiterhin, auch wenn wir die Prämisse D hinzufügen.

Die Regel der Synthesis scheint nicht immer in hohem Ansehen gestanden zu haben. So beklagt sich Platon in einer dunklen Passage seiner Schrift Phaidon über Gegner der Vernunft, die ein erstes Prinzip mit den Dingen, die daraus folgen, in einen Topf würfen. (Wenn sich aber einer an die Voraussetzung selbst hielte, würdest du den nicht gehen lassen und nicht eher antworten, bis du, was von ihr abgeleitet wird, betrachtet hättest, ob es miteinander stimmt oder nicht stimmt? Und solltest du dann von jener selbst Rechenschaft geben, würdest du sie nicht auf die gleiche Weise geben, [E] nämlich eine andere Voraussetzung wieder voraussetzend, welche dir eben von den höher liegenden die beste dünkte, bis du auf etwas Befriedigendes kämest, nicht aber untereinander mischend wie die Streitkünstler bald von dem ersten Grunde reden und bald von dem daraus abgeleiteten, wenn du nämlich irgend etwas, wie es wirklich ist, finden wolltest? Platon, Phaidon 101 d–e)

Wie dem auch sei, die Frage, ob A aus B und C folgt, hängt nicht im Geringsten davon ab, wie wir zu den Prämissen B und C gelangten oder ob diese Prämissen „erste Prinzipien“ oder „erste Voraussetzungen“ sind oder nicht oder ob wir neben den Prämissen B und D noch andere Informationen haben.

(3) Die Regeln (1) und (2) sagen uns nur, wie wir Argumente zu neuen Argumentketten zusammenfügen. Die folgenden Regeln dagegen sagen uns, wie wir neue Argumente mit anderen Prämissen und Konklusionen finden als denen, die wir bereits kennen.

Regel (3) ist die Regel zur Verwendung der reductio ad absurdum, die wir schon im 6. Kapitel kennengelernt haben (Wie wir Argumente verwenden). Wenn die Prämissen P, Q, R … zu einem Widerspruch führen, schließen wir daraus nicht (wenn wir genügend logisches Feingefühl aufbringen), dass wir den Widerspruch bewiesen haben, sondern nur, dass etwas mit den Prämissen nicht stimmt. Also versuchen wir es so: Wir behalten die Prämissen Q, R … und von diesen Prämissen gelangen wir womöglich zum kontradiktorischen Gegensatz der angenommenen Prämisse P. Wir haben diesen Schritt im 13. Kapitel vorexerziert.

Nehmen wir folgende Prämissen an:

Die meisten As sind Bs. Die meisten Bs sind Cs. Die meisten Cs sind As. Kein A ist ein BC.

Diese Aussagen ergeben zusammen eine Kontradiktion.

Denn wir können von den Prämissen:

Die meisten As sind Bs. Die meisten Bs sind Cs. Die meisten Cs sind As.

den kontradiktorischen Gegensatz zu der weggelassenen obigen Prämisse „Kein A ist BC“ ableiten:

Einige As sind BC.

Die Logik schreibt uns im Allgemeinen nicht vor, welche Prämissen wir beibehalten sollen, und gibt uns kein Verfahren an die Hand, genau die Prämisse herauszufischen und außen vor zu lassen, die wir verwerfen müssen. (Wenn das Schiff im Sinken begriffen ist, wissen wir, dass irgendwer wohl über Bord gehen wird, aber keine Logik verrät uns, wer.)

(3a) Von der Regel der reductio ad absurdum können wir die Regel der Kontraposition ableiten, die unserer Argumentation öfters aufhilft. Wenn wir aus A und B den Schluss C ziehen können, dann können wir von A und der Negation von C auf die Negation von B schließen. Denn wenn C aus A und B folgt, dann führt die Menge der Prämissen:

A, Nicht-C und B

zu einem Widerspruch – zwischen der Negation von C (schon als Prämisse gegeben) und der Behauptung C (die aus A und B ableitbar ist). Folglich müssen wir B verwerfen und auf die Negation von B schließen, wenn wir A und die Negation von C behaupten wollen.

(4) Es gibt noch eine Regel für die Bildung von Argumenten, die allzu evident anmutet: Unter der Annahme der Wahrheit der Prämissen A, B, C … können wir auf die Konklusion P schließen. Jetzt nehmen wir an, dass eine unserer Prämissen aus dem Vorrat entfällt, sagen wir B, und dass P aus den verbleibenden Prämissen A, C … nicht länger folgt. Einerlei, wir wissen, dass etwas aus A, C … folgt, so wie sie nun einmal dastehen, nämlich die mit B und P gebildete Implikation: Wir wissen: Aus den Prämissen A, C … folgt P, falls B wahr ist.

Beispiel:

„Alle Bücher auf dem Bücherbord sind blau eingebunden. Auf dem Bücherbord befindet sich eine Ausgabe von Caesars De Bello Gallico.“

Wir erhalten offenkundig die Konklusion: „Auf dem Bücherbord befindet sich eine Ausgabe von Caesars De Bello Gallico mit blauem Einband.“

Das Beispiel macht klar, dass wir die Konklusion aus nur einer Prämisse („Alle Bücher auf dem Bücherbors sind blau eingebunden“) ziehen können: „Falls es eine Ausgabe von Caesars De Bello Gallico unter den Büchern auf dem Bord gibt, dann gibt es unter den Büchern eine blau eingebundene Ausgabe von Caesars Schrift.“

Das Argument, das wir durch Anwendung der Regel (4) (von den Logikern auch Bedingungsregel genannt) erhalten, unterscheidet sich vom ursprünglichen Argument. In unserem Beispiel hat das Ausgangsargument zwei Prämissen mit der Konklusion, dass es eine Ausgabe von Caesars Schrift im blauen Einband auf dem Bücherbord gibt. Das Argument, das wir durch Anwendung der Bedingungsregel erhalten – das gültig sein muss, weil unser Ausgangsargument gültig war –, hat nur eine Prämisse, und diese ist anders als im Ausgangsargument mit der Konjunktion „falls“ gebildet.

(5) Dilemma. Dies ist einer der Fachbegriffe aus der Logik, die in die Umgangssprache eingingen, ohne dass seine fachliche Bedeutung gänzlich verblasst wäre. Die Regel gibt an, wie zwei Argumente verwoben werden können, die auf unterschiedlichem Weg zur selben Konklusion führen.

Nehmen wir an, der Schluss P folge in einem gültigen Argument aus den Prämissen A, B, C … und P folge ebenso aus den Prämissen D, E, F … Nun nehmen wir zusätzlich an, dass uns weder A noch D als Prämissen gegeben sind, sondern nur die Alternative, dass entweder A gilt oder D. Dann können wir von dieser Information zusammen mit den verbleibenden Prämissen B, C … und E, F … tatsächlich den Schluss auf P ziehen. Auf der einen Seite der Alternative folgt P aus A, B, C … und auf der anderen Seite aus D, E, F … Wie dem auch sei: P folgt aus B, C … und E, F … plus der Alternative A oder D.

Beispiel:

P: Entweder wird B das Wasser in seiner Wasserflasche trinken oder er wird es nicht trinken.

Alternative I:
Q: B wird das Wasser aus seiner Wasserflasche trinken.
R: Das Wasser in Bs Wasserflasche ist völlig versalzen und B ist ernsthaft dehydriert.
S: Jeder, der völlig versalzenes Wasser trinkt und ernsthaft dehydriert ist, verdurstet.
T: B wird verdursten.

Alternative II:
V: B wird das Wasser in seiner Wasserflasche nicht trinken.
W: Wenn B das Wasser in seiner Wasserflasche nicht trinkt, wird er in der Wüste nichts zu trinken haben.
X: Wenn B kein Wasser bekommt, wird er verdursten.
T: B wird verdursten.

Nach Alternative I folgern wir T aus Q, R und S. Nach Alternative II folgern wir T aus V, W und X. Da P (wonach entweder Q oder V wahr ist) so oder so offensichtlich ist, können wir T aus der Menge der Prämissen R, S, W und X folgern – auch wenn wir nicht wissen, welche der Prämissen Q oder V wahr ist.