Peter Geach, Reason and Argument XII (mit deutscher Übersetzung)
12. Uses of Diagrams to Test Validity of Schemata
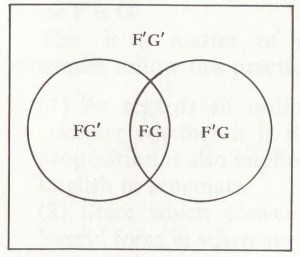
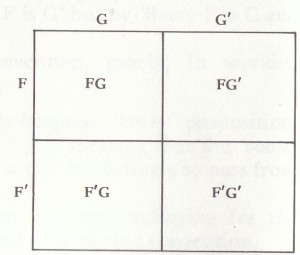
If we have two predicates applying in our Universe, we may have things of four different kinds described by means of these predicates: for a given thing a in the universe there are four possibilities
1. a is F and a is G
2. a is F and a is G’
3. a is F’ and a is G
4. a is F’ and a is G’
So the object may come in one of four different cells or compartments of the Universe.
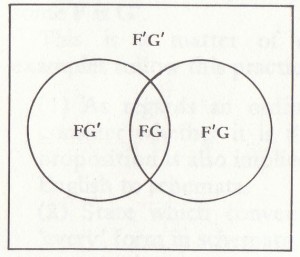
Venn diagram Lewis Carroll diagram
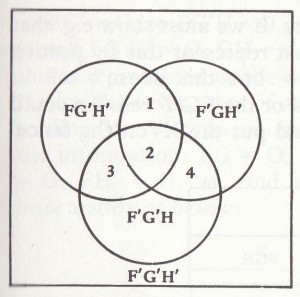
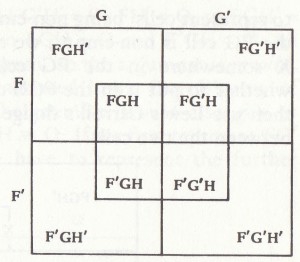
The shape of the cells clearly doesn’t matter logically, only the exhaustive division of the Universe into four cells. If we have three predicates we need eight cells:
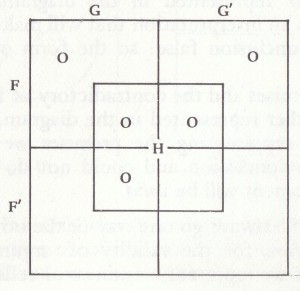
Venn diagram Lewis Carroll diagram
Cell 1 for FGH’; Cell 2 for FGH;
Cell 3 for FG’H; Cell 4 for F’GH’
For four predicates we need sixteen cells; and so on.
So far the diagrams tell us nothing about the Universe — only shows us a logical possibility of classifying its contents. To show propositions in a diagram we put a mark in a cell to show that it is empty (0) or non-empty (X). If we are given premises and a conclusion:
1. If the premises and the contradictory of the conclusion canbe togetherrepresented in the diagram, this will be because there is an interpretation that will make the premises true and the conclusion false: so the form of argument is invalid.
2. If the premises and the contradictory of the conclusion cannotbe together represented in the diagram, then this will be because in representing the premises we have already represented the conclusion and could not do otherwise: so the form of argument will be valid.
The result will always go one way or the other, so this is a decision procedurefor the validity of argument-schemata.
It pays off if we represent emptiness of cells before trying to represent cells’ being non-empty. If we must show e.g. that the FG cell is non-empty, we must represent this by putting X somewhere in the FG cell — but this doesn’t tell us whether to put it in the FGH cell or the FGH’ cell. We could then use Lewis Carroll’s dodge and put the X ‘on the fence’ between the two cells:
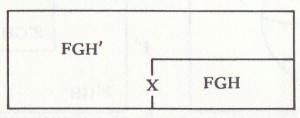
but we may not need to do this if the FGH cell is already marked as empty, since a X and a O cannot go into the same (undivided) cell: we then must mark the diagram thus:
Examples of valid and invalid schemata:
Every F is G ; every F is H; ergo some G is H.
In existential form the premises are: FG’ = O, FH’ = O, and the contradictory of the conclusion is: GH = O. Let us see how to represent this information.
FG’ = O, so FG’H = O and FG’H’ = O. FH’ = O, so FGH’ = O and FG’H’ = O. GH = O, so FGH = O and F’GH = O. All this is represented in the diagram, so the argument is invalid. Notice, however, that if we adopted Lewis Carroll’s way of reading ‘every’ proposition the premises would also give us the information: FG ≠ O, FH ≠ O. If we first represent FG’ = O, FH’ = O, we find we have to represent the further information as below:
(After inserting the Os, there is only one place left to put the X within the FG cell or the FH cell.)
We now cannot mark the GH cell as empty, so the argument is valid. This is no surprise, because the Lewis Carroll way of reading ‘every’ propositions makes them more informative, and a conclusion that doesn’t validly follow when we have less information may follow when we have more. (Can a conclusion ever follow from more limited information, but be seen not to follow when we have further information?)
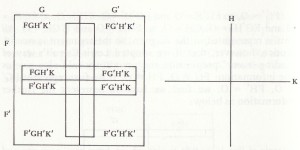
It is hard to draw four-term Venn diagrams (impossible with overlapping circles), but quite easy to draw four-term Lewis Carroll diagrams, thus:
(i.e. the inside large vertical rectangle is the H cell, the inside large horizontal compartment is the K cell).
If we wish to represent a singular proposition of form ‘a is FG’ say, then we simply use an asterisk instead of an X. Since an asterisk contains an X, this is meant to show that a cell containing an asterisk is marked as non-empty. The only extra rule we need is that since an individual cannot belong to two separate classes (e.g. a cannot be both FG and F’GH) we must put only one asterisk in the diagram if only one individual name figures in the premises — whereas there is no ban on inserting several Xs in the diagram.
12. Die Verwendung von Diagrammen zur Überprüfung der Gültigkeit von logischen Schemata
Wenn wir zwei Prädikate in unserem Universum haben, könnten wir vier Gegenstände verschiedener Art unterscheiden, die mittels dieser Prädikate beschrieben werden: Für einen in unserem Universum gegebenen Gegenstand a gelten vier Möglichkeiten:
1. a ist F und a ist G
2. a ist F und a ist G’
3. a ist F’ und a ist G
4. a ist F’ und a ist G’
Demnach kann der Gegenstand a in einem von vier verschiedenen Zellen oder Abteilungen des Universums auftauchen.
Venn-Diagramm Diagramm von Lewis Carroll
Der Umriss der Zellen tut logischerweise nichts zur Sache, der wesentliche Punkt ist die vollständige Aufteilung des Universums in vier Zellen. Wenn wir drei Prädikate haben, benötigen wir acht Zellen:
Venn-Diagramm Diagramm von Lewis Carroll
Zelle 1 für FGH’; Zelle 2 für FGH;
Zelle 3 für FG’H’; Zell 4 für FG’H
Zelle 5 für F’GH’; Zelle 6 für F’GH
Zelle 7 für F’G’H’; Zelle 8 für F’G’H
Für vier Prädikate benötigen wir 16 Zellen usw., x2, wenn x die Anzahl der Prädikate darstellen.
In dieser Form verraten uns die Diagramme keine definitiven Inhalte über das Universum – sie zeigen uns nur die logischen Möglichkeiten, wie wir die Inhalte anordnen oder klassifizieren können. Wenn wir Aussagen in einem Diagramm einzeichnen wollen, versehen wir eine Zelle mit dem Zeichen 0, um anzuzeigen, dass sie leer ist, und mit dem Zeichen X, um anzuzeigen, dass sie nicht leer ist. Wenn wir Prämissen und eine Konklusion vor uns haben, gehen wir wie folgt vor:
1. Wenn sowohl die Prämissen als auch die Negation der Konklusion im Diagramm dargestellt werden können, liegt das offensichtlich daran, dass eine Interpretation der beiden Aussagen die Prämisse wahr macht und die Konklusion falsch: Demnach ist die Form des Arguments ungültig.
2. Wenn dagegen die Prämissen und die Konklusion nicht gleichzeitig im Diagramm dargestellt werden können, liegt das offensichtlich daran, dass in der Darstellung der Prämissen die Konklusion bereits enthalten war: Demnach ist die Form des Arguments gültig.
Eine Überprüfung der Gültigkeit von Argumenten mittels solcher Diagramme kommt immer zu dem einen oder dem anderen Ergebnis. Das heißt, es handelt sich um ein Entscheidungsverfahren in Bezug auf die Gültigkeit von Argumentformen.
Es lohnt sich, zuerst die leeren Zellen zu markieren, bevor wir die belegten Zellen zu markieren versuchen. Wenn wir zum Beispiel zeigen müssen, das die FG-Zelle nicht leer ist, müssen wir dies dadurch anzeigen, dass wir ein X mitten in die Zelle platzieren – doch das sagt uns noch nichts darüber, ob wir berechtigt sind die FGH-Zelle oder die FGH’-Zelle ebenso zu markieren. Wir können im Zweifelsfalle den Trick von Lewis Carroll anwenden und das X genau auf der Grenzlinie platzieren:
Allerdings dürfen wir das nicht tun, wenn die FGH-Zelle bereits als leer markiert ist, denn die Zeichen 0 und X dürfen nicht in derselben Zelle vorkommen. Folglich müssen wir das Diagramm folgendermaßen markieren:
Beispiele für gültige und ungültige Schemata:
Jedes F ist G. Jedes F ist H. Ergo: Einige G sind H.
In quantifizierter Schreibweise stellen wir die Prämissen so dar: FG’ = 0. FH’ = 0. Die Kontradiktion der Konklusion sieht so aus: GH = 0. Dieses Argument können wir in ein Diagramm fassen:
FG’ = 0, also FG’H = 0 und FG’H’ = 0. FH’ = 0, also FGH’ = 0 und FG’H’ = 0. GH = 0, also FGH = 0 und F’GH = 0. Alle diese quantifizierten Aussagen sind in dem Diagramm eingeschrieben, das heißt: Die Argumente sind alle ungültig. Würden wir die Lesart von Lewis Carroll benutzen, gäben uns die Prämissen noch folgende Informationen: FG ≠ 0, FH ≠ 0. Wenn wir zunächst die Aussagen FG’ = 0 und FH’ = 0 darstellen, werden wir die restlichen Informationen in folgender Weise in das Diagramm schreiben:
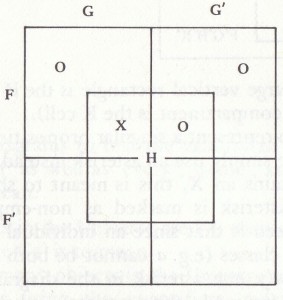
(Nachdem die Nullen eingetragen haben, gibt es nur noch einen Platz in der FG-Zelle oder der FH-Zelle, in der wir das X markieren können.)
Wir können die GH-Zelle nicht mit einer Null als leer kennzeichnen, also ist das Argument gültig. Das ist keine Überraschung, weil die Lesart von Lewis Carroll für die Aussagen mit dem Quantor „einige“ mher Infiormatioonen enthält, und eine Konklusion, die wir bei weniger Information nicht schlüssig folgern können, lässt sich eher folgern, wenn wir mehr Information zur Verfügung haben. (Kann eine Konklusion jemals aufgrund einer begrenzten Information folgen, aber nicht folgen, wenn uns mehr Information zur Verfügung steht?)
Es ist ziemlich schwierig, Venn-Diagramme für vier Prädikatterme zu bilden (mittels überlappender Kreise funktioniert es gar nicht). Aber mit den Diagrammen von Lewis Carroll ist es ziemlich leicht:
(Beachte: Das innere lange Rechteck in der Vertikalen ist die H-Zelle, das innere lange Rechteck in der Horizontalen ist die K-Zelle.)
Wenn wir eine singuläre Aussage der Form „a ist FG“ im Diagramm abbilden wollen, gebrauchen wir einfach ein Sternchen anstelle des X, um zu markieren, dass die Zelle nicht leer ist – ein Sternchen enthält ja ein X. Die einzige Zusatzregel, die wir anwenden müssen: Da eine Individuenkonstante wie a nicht gleichzeitig zwei verschiedenen Klassen angehören kann (zum Beispiel kann a nicht beides sein: FG und F’GH), dürfen wir immer nur ein einziges Sternchen pro Diagramm verwenden, wenn nur ein einziger Name für einen Gegenstand in den Prämissen auftaucht – dagegen steht es uns frei, mehrere X in ein Diagramm einzuschreiben.